MTH 202 SOLUTION

Question 1
Let a function f: R®R be defined by
f(x) =2x3 + 7 Show that f is bijective.
Solution:
f is one-to-one
Let f(x1) = 2 x13 + 7 and f(x2) = 2 x23 + 7
By the definition we know that,

f(x1) = f(x2) for x1 , x2 Î R
2 x13 + 7 = 2 x23 + 7
2 x13 - 2 x23 = 7 – 7
2( x13 - x23 ) = 0
x13 - x23 = 0
(x1 - x2)( x12 + 2x1 x2 + x22) = 0
x1 - x2 = 0 ; x12 + 2x1 x2 + x22 = 0
x1 = x2 (The second equation gives no real solution)

Accordingly f is one-to-one.

f is onto
f(x) =2x3 + 7

let y Î R. We search for x Î R such that

f(x) = y
2x3 + 7 = y
x3 = OR x =

f(x) = f [ ]

f(x) = 2 + 7 = y – 7 + 7
f(x) = y

Thus f is a Bijective

Question 2;
Find the sum of the series whose nth term is .
Solution

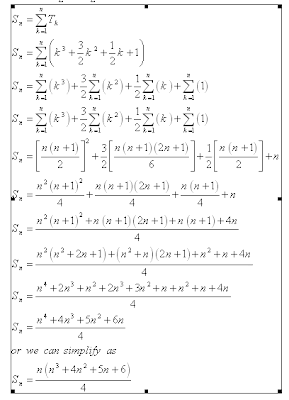
Tk =
Sn =
Sn = ( )

Sn =
Sn =

After simplifying we the Sum of Sn

Sn =




Question: Find the sum of the series whose nth term is .